数あるExcel関数の中でも、最頻出ともいえるVLOOKUP関数は、すでに実務で活用されている方も多いでしょう。lookupは「調べる」という意味の英単語で、これに「縦方向・垂直(vertical)」を表す『v』を冠した、検索関数の代表格です。
基本的な構文は
=VLOOKUP(検索値,範囲,列番号,[検索の型]) で、検索値に応じた返り値を探し出します。
※[検索の型]0=false(完全一致), 1=true(近似一致) は省略可能
例えば以下のシートでは、

セルC10に =VLOOKUP(C10,list,2,0)と入力することで、目的地に応じた地下鉄の片道運賃を、運賃表の中から検索することができます。
この場合、”検索値”が目的地、”範囲”が検索をかけるべき運賃表(listという名前をつけました)、その運賃表の”列番号”2列目が返り値で、完全一致する返り値のみを取り出します。
ここまでがVLOOKUP関数の基本の型ですが、実務の現場では、より複雑な条件分岐を求められる場面が出てきます。条件分岐はプログラミング(VBA)が得意とする領域ですが、2つか3つの条件分岐までであれば、わざわざプログラムを書く必要はありません。VLOOKUPの重ねワザで条件分岐をさせる事例について、次に具体的にみていきましょう。
大都市圏の複雑な地下鉄乗車賃を、VLOOKUPの重ねワザのみで正確に取得
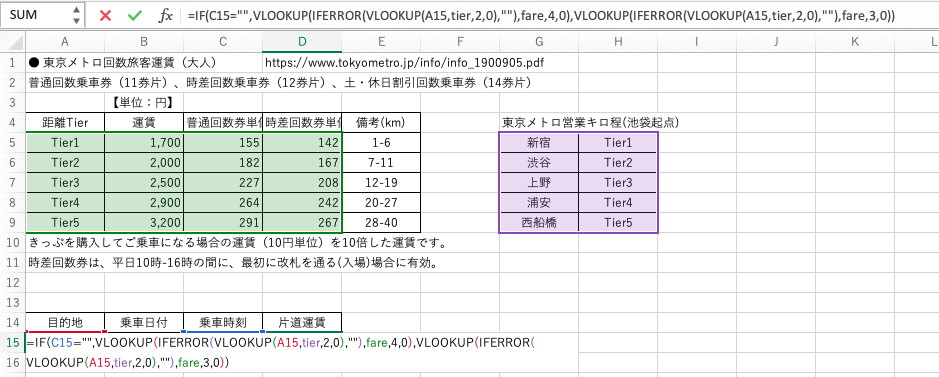
東京・大阪・名古屋などの大都市圏では、地下鉄が網の目のように張り巡らされており、1つの目的地に複数の方法で到達することができます。そのため、いわゆる「料金表」という一覧シートで運賃をまとめることはなく、「キロ呈運賃制」としているところがほとんどです。たとえば、東京メトロでは、乗車距離に応じて、(1)1~6km、(2)7~11km、(3)12~19km、(4)20~27km、(5)28~40kmと5段階の運賃設定をしています。その上、交通系ICカードを利用した場合ときっぷを買う場合で金額が異なったり、朝10時-夕4時までに改札を通る時に使える「時差割引回数券」があったり、同じ目的地でも、運賃が変わる複数の条件が存在します。この条件を正確に分岐させるにはどのようにしたら良いでしょうか?

たとえば、東京・池袋に本社があるX商事では、営業マンがひんぱんに通うクライアントのところまでの移動交通費を、経費削減のため、回数券で渡すようにしています。さらに、平日営業時間内での得意先訪問であれば、朝10時-夕4時まで有効な、時差割引回数券がほぼ利用できるため、時差券で支給することを基本としています。朝10時-夕4時以外の時間帯で移動が必要な場合には、社員からの申告で普通回数券を利用するものとします。このケースの片道運賃を正確に算出するためのシートが上図となります。
この表の中の「片道運賃」の欄、セルC15には、次の計算式が入っています。
=IF(C15="",VLOOKUP(IFERROR(VLOOKUP(A15,tier,2,0),""),fare,4,0),VLOOKUP(IFERROR(VLOOKUP(A15,tier,2,0),""),fare,3,0))
この計算式で参照する検索リストは2つ。
1つめは、池袋本社を起点として、各営業先が東京メトロ・キロ呈運賃表のどの段階(km)にあるかを示すリスト(tierと名づけました)。
2つめは、キロ呈運賃表5段階ごとの、普通回数券と時差割引回数券の価格差を示すリストです(fareと名づけました)。
そして、片道運賃欄の左どなり(C列)には、時差割引券が利用できない時刻に移動する場合のみその時刻を申告し、その場合には普通回数券の価格を取り出します。乗車時刻の申告がない場合には、時差割引回数券の価格を取り出すように計算結果を分岐させました。
まとめ:2つや3つ程度の条件分岐であれば、VBA不要。VLOOKUPの重ねワザで、正確な検索結果を獲得しましょう。
経費精算に限らず、在庫管理やアルバイト・パートさんのシフト管理など、複数条件をかけ合わせなければ正確な解答を得られないケースは、ビジネスの現場で多くみられます。すぐにVBAで条件分岐プログラムを組めるのであれば良いですが、それが難しい場合には、複数の関数をからめあわせることで、条件分岐プログラムと同等の結果を簡単に導き出すことができます。検索条件が多岐に渡っていても、頭を抱えこむことなく、まずは冷静に検索条件を整理してみましょう。業務効率化のキモは、この「正確な検索リストの整備」にありますよ。